Reasoned PHP

Using logic to run your programs backwards!

This is a transcript of a talk I gave at the Berlin PHP usergroup in August 2014.

Logic

This presentation is going to be about using logic to run your programs backwards. Let’s begin with talking about logic.

One of the first logicians was Aristotle, a few years before Christ. He came up with syllogisms — logical statements — that would look something like this:

I am a human.

Every human is mortal.

Therefore, I am mortal.

And by combining these statements, one could reach logical conclusions. Which would allow truths to be derived.

Then christianity happened, and there wasn’t really any progress in science and philosophy for… well, a while.

But then, in the 1600s, Leibnitz not only independently invented calculus (next to Newton), but also discovered many of the concepts that would play an important role in the formalisation of logic.

His calculus ratiocinator is an attempt at creating a universal language to describe human thought. He is famous for suggesting that truths should be calculated.

In the 1800s, a lot of progress was made on the logic front. Boole created boolean algebra. De Morgan published De Morgan’s laws. Both of these systems would allow translations to be made between logical statements, and they laid the groundwork for electronics.

Frege wrote the Begriffsschrift, introducing for the first time a formal logic that included a notion of functions and variables. This new method would form the basis for most of early 20th century mathematical work.

In 1935, Gentzen created not one, but two new formulations of logic¹: Natural deduction and the sequent calculus. It can be described in terms of a few simple rules.

At the same time, Church was trying to prove something about logic and accidentally invented the simply typed lambda calculus: The first functional programming language and it even has a type system!

This turned out to be a formalization of computation and thus remains one of the most commonly used ways of describing computers on the most fundamental level.

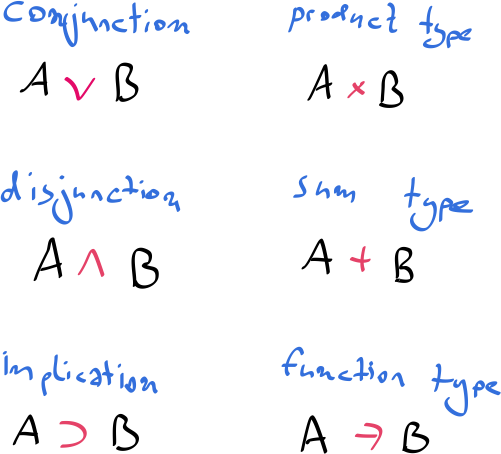
What is amazing however is that when the descriptions of natural deduction and the simply typed lambda calculus are compared, they appear to be identical! And that’s because they are identical! Logical proofs directly correspond to the types in programs!

This is what is known as the curry-howard isomorphism, and it shows us that there is a very strong link between logic and computation.

Programs

So let’s talk about programs. The way I tend to think about programs is as black boxes. You put things in on one end, stuff comes out on the other end. For the same things you put in, you will always get the same things out. It is deterministic in that sense.

In pure functional programming this is true for every function. But even if you don’t care about functional programming, this is still true at the macro scale. Your program as a whole is deterministic.

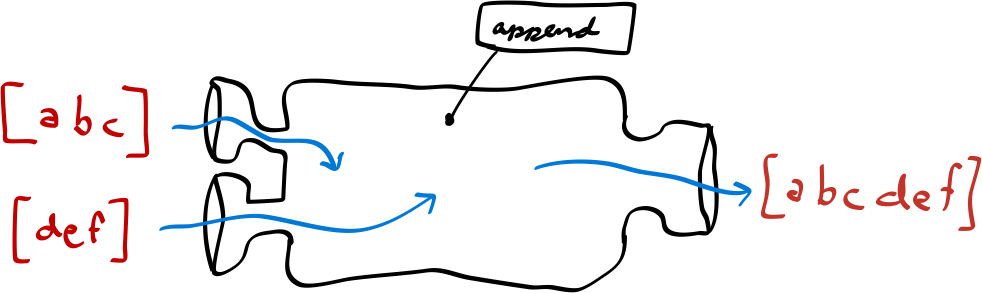
So let’s take a function append for example. You give it two lists as inputs, it produces a list as an output. The output list is the concatenation of the two input lists.

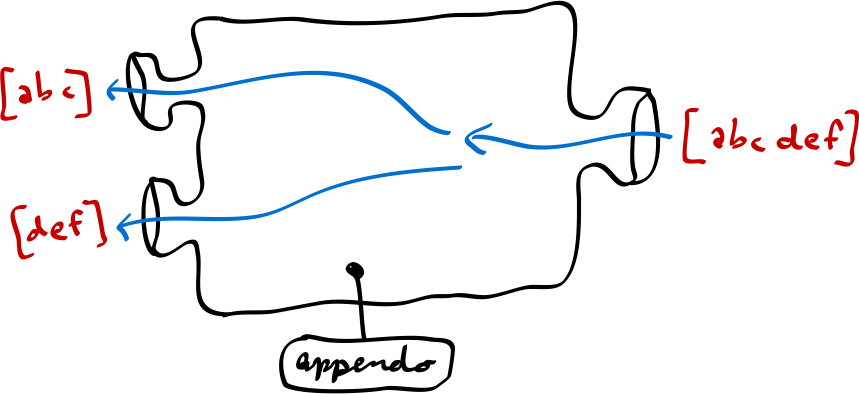
But would it be possible to reverse this process? Could we flip the inputs and the outputs, and ask “give me the inputs that when concatenated produce this output list”?

The laws of physics do not prevent the rules to be reversed, apart from the law of entropy. So let’s fight entropy.

The actual problem here is that there is more than one possible answer to the question. There are multiple ways in which two lists could create the provided output list.

And as a matter of fact, we can enumerate all of the possibilities. And from looking at them, we can tell that there is some sort of relationship between the two inputs. As one of them grows, the other one shrinks.

And usually in any slightly more complicated program, we don’t just have a list of possibilities. It is a tree. A tree that branches out, that can be traversed and searched.

The type of programming that I am describing is constraint logic programming. More specifically, constraint logic programming over the domain of trees.

The execution of the program corresponds to a search over the tree. You are searching for an answer that will satisfy the given constraints. And this search corresponds to a search for a constructive logical proof.

In order to construct this tree, the program needs to be written in a particular kind of way. The way it is done is by redefining equality, or rather, assignment.

In most programming languages, assignment is a uni-directional construct. A value is assigned to a variable. It only goes one way.

However, if you extend this notion to a bi-directional relationship in which the order of statements does not matter, you gain reversibility.

At this point you no longer have inputs and outputs. You just have pieces of information that are related to each other. This is why this form of programming is also known as relational programming².

Another important piece of the puzzle is the tree search and the matching of trees against each other. This happens through an algorithm called unification.

You can think of unification as a way of taking two trees — or lists of lists — and matching them against each other. The trees can contain “holes” which are unbound variables. When matching the trees against each other, they can fill each other’s holes. If there is no contradiction, then the trees unify.

Another way to think about it is a bi-directional pattern match.

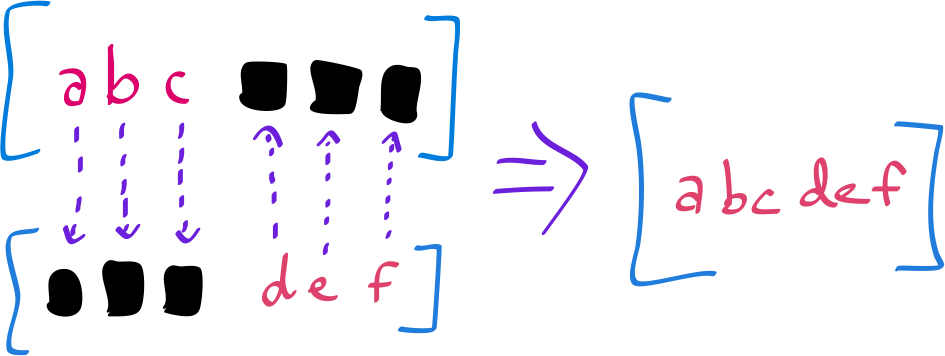
Reasoned PHP

This brings us to a system that I have been working on. It is called Reasoned PHP.

Reasoned PHP is a logic programming system written in PHP. It is a port of miniKanren into PHP. An embedded language for relational programming.

function appendᵒ($l, $s, $out) {
    return condᵉ([
        [≡($l, []), ≡($s, $out)],
        [fresh_all(($a, $d, $res) ==> [
            consᵒ($a, $d, $l),
            consᵒ($a, $res, $out),
            appendᵒ($d, $s, $res),
        ])],
    ]);
}

This is what the code looks like. Your first thought might be “omg that’s so ugly”, to which I will answer: What did you expect? It’s PHP.

Your second thought might be “omg unicode function names”. Yep. Amazing, isn’t it?

If you wanted to actually call this appendᵒ relation, here is how you would do it:

run٭($q ==>
    appendᵒ([1, 2, 3], [4, 5, 6], $q));

So let’s suppose we have a relation called memberᵒ that tells you if a variable $x is a member of the list $list:

memberᵒ($x, $list)

We can now ask this relation questions, such as “is 2 a member of the list [1, 2, 3]?”, to which it will respond with _.0 which is a strange way of saying yes.

memberᵒ(2, [1, 2, 3])
// => _.0

That is not very interesting yet. Instead we could ask: is the unbound variable $x a member of the list [1, 2, 3]? In this case, it will answer “yes, and by the way, these are the possible values it could take!”

memberᵒ($x, [1, 2, 3])
// => 1, 2, 3

Now, you can also combine these statements. Is $x a member of [1, 2, 3] and of [3, 4, 5]?

memberᵒ($x, [1, 2, 3])
memberᵒ($x, [3, 4, 5])
// => 3

And sure enough, it actually figured out that there is only one value that is a member of both lists: 3. So without explicitly defining an intersection operation, the intersection emerges from the tree search.

Cool stuff

I want to emphasise that this is a general programming technique and you can model almost any computation in this way. And by doing so, you will be able to run any program that is written in a relational manner backwards!

Nevertheless, there are certain problems where this approach fits particularly well. I would like to show you some of them.

The first one is mathematical formulae. A formula is just a tree of terms and most of calculus does not actually involve calculation at all. It is just symbolic manipulation of symbols. And that’s precisely what prolog and other logic programming systems excel at.

Here is an example of symbolic differentiation³.

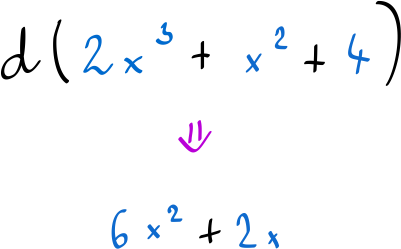
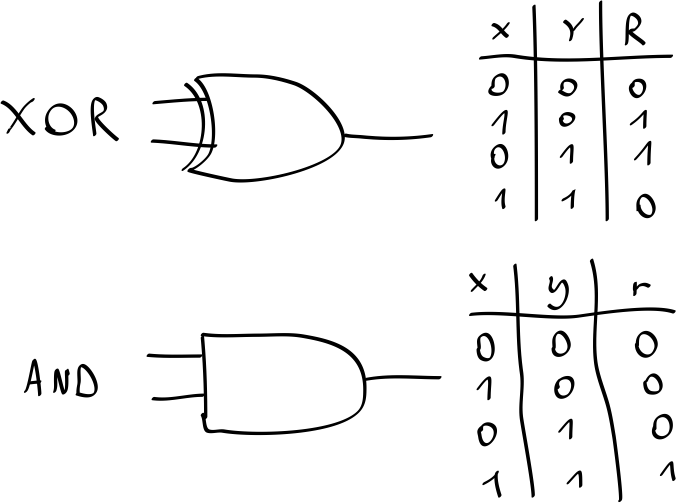
In electronics you have logic gates that react to electrical signals in certain ways. A logic gate can be depicted with a symbol as often used in circuit schematics. But it can also be described in terms of a truth table.

The truth table describes the logical relation between the input bits and the output bit. It is a function. As such, it can be implemented as a bi-directional relation.

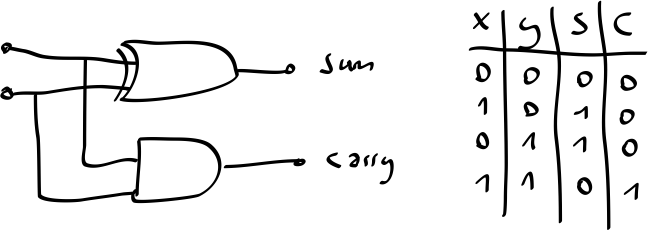
It is possible to combine these two gates to form a so-called half-adder. The half-adder also has a truth table. And thus also can be a relation.

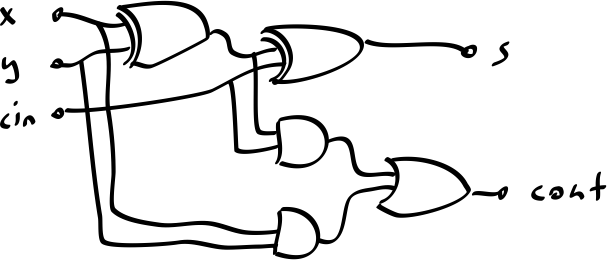
By combining two half-adders, you can create a full-adder. It allows you to add two binary digits. Chaining n full adders allows you to add two n-bit binary numbers. n corresponds to the amount of binary digits. And that’s really what the ALU inside of your computer does.

This circuit is reversible.

Normally if you think of arithmetic, it is a function. Two numbers go into the addition operator, the sum comes out on the other end.

If you implement arithmetic as a relation, you can ask questions such as “give me all the numbers that add up to 5”. The system will enumerate them⁴!

Moving up from hardware to software, we have compilers. A compiler is a program that reads the source code of another program and compiles it down to machine code.

If you implement a compiler in a relational way, you get not only a compiler, but also a decompiler. That means that if you’re lucky, you will be able to take an arbitrary chunk of machine code and translate it back into some sort of source code!

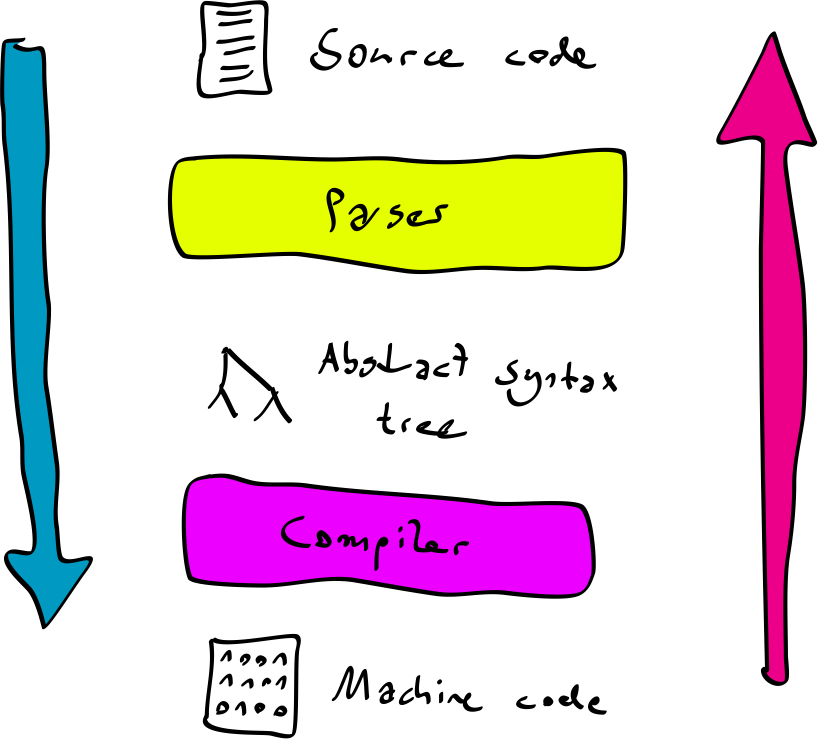
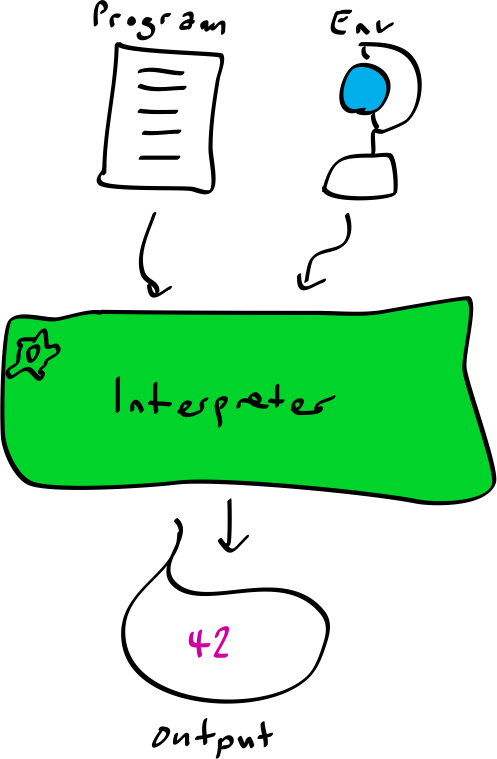
This becomes even more fun when you write a relational interpreter. An interpreter is a program that reads the source code of another program and executes it. Then sometimes produces an output.

With a relational interpreter you can not just feed it some input and see the output. You can ask it questions such as “give me all of the programs that evaluate to 42”. The system will enumerate them!

This is extremely powerful. It is almost like doing TDD, but without writing the code. The tests constrain what the program must do. The proof search will try to find a program that satisfies those constraints. It has actually been possible to synthesise small programs using this technique.

One very cool aspect of unbound variables is that you can use them multiple times. This allows you to formulate a question such as “give me a program that when executed outputs its own source code”. This is what is known as a quine, and a relational interpreter will happily generate quines for you⁵!

eval_expᵒ($q, [], $q)

// => ((lambda (_.0) (list _.0 (list 'quote _.0)))
//     '(lambda (_.0) (list _.0 (list 'quote _.0)))

But you can do something even better than that. You can ask the interpreter to produce a program $x that evaluates to the source code of a program $y. And the program $y should then evaluate to the source code of $x again. This is what is known as a twine, and a relational interpreter will happily generate twines for you!

eval_expᵒ($x, [], $y)
eval_expᵒ($y, [], $x)

// => ((lambda (_.0)
//      (list 'quote (list _.0 (list 'quote _.0))))
//     '(lambda (_.0) (list 'quote (list _.0 (list 'quote _.0)))))
//
//     ((lambda (_.0) (list 'quote (list _.0 (list 'quote _.0))))
//     '(lambda (_.0) (list 'quote (list _.0 (list 'quote _.0)))))

µKanren

How much code does it take to implement the basic mechanisms of a logic programming system? One of the smallest ones, that Reasoned PHP is in fact based upon, is called µKanren.

It consists of ~50 lines of code.

It’s amazing how little code is needed to build a logic programming system.

1. From Propositions as Types by Philip Wadler ↩

2. A term popularised by William Byrd and miniKanren ↩

3. From Clause and Effect by William Clocksin ↩

4. This number system is described in The Reasoned Schemer and is lovingly referred to as “Oleg Numbers” ↩

5. From Quine Generation via Relational Interpreters by Byrd et al.↩

References

• Propositions as Types
  Philip Wadler

• µKanren
  Jason Hemann, Daniel Friedman

• Quine Generation via Relational Interpreters
  William Byrd, Eric Holk, Daniel Friedman

• The Reasoned Schemer
  Daniel Friedman, William Byrd, Oleg Kiselyov

• Clause and Effect
  William Clocksin

• The Annotated Turing
  Charles Petzold

• Code
  Charles Petzold

• Logicomix
  Apostolos Doxiadis, Christos Papadimitriou